Kamis, 30 Agustus 2012

Bangun Ruang

Bangun Ruang

 Bangun ruang merupakan bangun matematika (matematika) yang memiliki isi atau volume. Bangun ruang dalam matematika dibagi menjadi beberapa bangun ruang yakni sisi, rusuk dan titik sudut. Sisi merupakan bidang pada bangun ruang yang membatasi antara bangun ruang dengan ruangan di sekitarnya, Rusuk merupakan pertemuan dua sisi yang berupa ruas garis pada bangun ruang sedangkan Titik sudut adalah titik dari hasil pertemuan rusuk yang berjumlah tiga atau lebih.
Pada umumnya bangun ruang yang telah kita kenal adalah balok, kubus, prisma, limas, kerucut, tabung dan bola. Pada setiap bangun ruang tersebut mempunyai rumusan dalam menghitung luas maupun isi/volumenya.
Matematika bangun ruang

KUBUS

Kubus adalah suatu bangun ruang yang dibatasi oleh enam buah sisi berbentuk persegi yang kongruen
Bangun berbentuk kubus dapat kita jumpai dalam kehidupan sehari-hari
Pada gambar tampak :
  1. Dadu yang berbentuk kubus
  2. Gambar kubus yang terdiri dari enam buah bidang yag berbentuk persegi yang kongruen
  3. Kerangka kubus yang terbuat dari logam (yang disebut rusuk) terdiri dari 12 rusuk kubus yang sama panjang
Perhatikan gambar berikut !
     
 Dadu berbentuk kubus
 
Gambar Kubus
Kerangka Kubus

Terdapat 6 buah sisi kongruen yang berbentuk persegi yang akan membatasi KUBUS, posisinya adalah:   
  1. sisi alas
  2. sisi depan
  3. sisi atas
  4. sisi belakang
  5. sisi kiri
  6. sisi kanan




Penamaan kubus disesuaikan dengan sisi alas dan sisi atas.
Jika sisi alas kubus ABCD, dan sisi atas kubus EFGH, maka kubus tersebut dinamakan kubus ABCD.EFGH
Rumus Kubus
- Volume : Sisi pertama dikali sisi kedua dikali sisi ketiga (S pangkat 3)
- Luas Alas : Sisi pertama dikalo sisi kedua (S pangkat 2)
Q

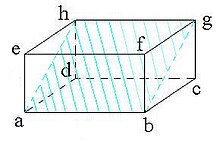
Balok

Balok.JPG
Balok adalah bangun ruang tiga dimensi yang dibentuk oleh tiga pasang persegi atau persegi panjang, dengan paling tidak satu pasang diantaranya berukuran berbeda. Balok memiliki 6 sisi, 12 rusuk dan 8 titik sudut. Balok yang dibentuk oleh enam persegi sama dan sebangun disebut sebagai kubus

Elemen balok

  • Panjang 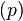(p) adalah rusuk terpanjang dari alas balok.
  • Lebar 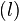(l) adalah rusuk terpendek dari sisi alas balok.
  • Tinggi (t) adalah rusuk yang tegak lurus terhadap panjang dan lebar balok.

Rumus balok


Diagonal Ruang b-h dan
Diagonal Bidang b-g

Bidang Diagonal a-b-g-h

Luas permukaan

L = 2\cdot (p\cdot l + p\cdot t + l\cdot t)

Volume

V = p\cdot l \cdot t

Panjang diagonal ruang

d_R = \sqrt{(p^2+l^2+t^2)}

Panjang diagonal bidang

d_{B1} = \sqrt{(s^2+s^2)}
d_{B2} = \sqrt{(s^2+s^2)}
d_{B3} = \sqrt{(s^2+s^2)}

Luas bidang diagonal

L_{B1} = d_{B1}\cdot t
L_{B2} = d_{B2}\cdot l
L_{B3} = d_{B3}\cdot p

Bola (geometri)

Bangun bola
dengan jari-jari r
Untuk kegunaan lain dari Bola, lihat bola
Dalam geometri, bola adalah bangun ruang tiga dimensi yang dibentuk olehtak terhingga linkaran berjari-jari sama panjang dan berpusat pada satu titik yang sama. Bola hanya memiliki 1 sisi.

Rumus bola

Luas permukaan

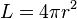
L = 4 \pi r^2 \,

Volume

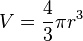
V = \frac{4}{3}\pi r^3

BANGUN RUANG PRISMA

prismaPada materi sebelumnya kita telah membahas dua buah bbangun ruang yaitu kubus dan balok. Nah, untuk materi sekarang kita akan mencoba membahas tentang bangun ruang lainnya yaitu prisma. Seperti apakah bangun prisma itu? Bagaimanakah menghitung volume dan luas permukaan bangun tersebut? Untuk mempelajarinya silahkan menyimak materi berikut.

Pengertian Prisma

Suatu bangun ruang yang bentuk dan ukuran sisi atas dengan sisi bawah sama serta rusuk-rusuk tegak yang sejajar disebut prisma.
Sebuah bangun prisma ditentukan oleh bentuk alasnya. Maksudnya bahwa penamaan suatu prisma berdasarkan bentuk alasnya, contohnya, suatu bangun prisma yang alasnya  berbentuk segitiga maka dinamakan prisma segitiga, prisma yang alasnya  berbentuk segiempat maka dinamakan prisma segiempat, prisma yang alasnya  berbentuk segi-lima maka dinamakan prisma segi-lima, dan seterunya.

Jenis-Jenis Prisma

Seperti yang dijelaskan di atas bahwa penamaan prisma detentukan oleh bentuk alasnya maka prisma  ada banyak jenis. Berikut adalah beberapa diantaranya:

1. Prisma segitiga

Prisma segitiga adalah prisma yang bentuk alas dan atapnya berbentuk segitiga. Unsur yang dimiliki prisma segitiga ABC.DEF adalah sebagai berikut:
  • Sisi/bidang = memiliki 5 sisi atau bidang yaitu sisi alas (ABC), sisi atas (DEF), dan tiga sisi tegak (ABED, BCFE, ACFD)
  • Rusuk = memiliki 9 rusuk yaitu rusuk alas (AB, BC, AC), rusuk atas (DE, EF, DF) Rusuk tegak (AD, BE, dan CF)
  • Titik Sudut = memiliki 8 titik sudut yaitu titik sudut A, B, C, D, E, F, G dan H.

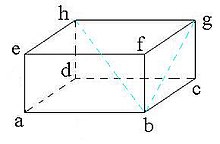
2. Prisma Segiempat

Prisma segiempat adalah prisma yang bentuk alas dan atapnya berbentuk segiempat. Unsur yang dimiliki prisma segiempat ABCD.EFGH adalah sebagai berikut:
  • Sisi/bidang = memiliki 6 sisi atau bidang yaitu sisi alas (ABCD), sisi atas (EFGH) dan empat sisi tegak ABFE, BCHF, CDGH dan ADGE
  • Rusuk = memiliki 12 rusuk yaitu rusuk alas (AB, BC, CD, DA), rusuk atas (EF, FH, GH, EG), rusuk tegak (EA, FB, HC, GD)
  • Titik Sudut = memiliki 8 titik sudut yaitu titik sudut A, B, C, D, E, F, G dan H.

3. Prisma Segi-lima

Prisma segi-lima adalah prisma yang bentuk alas dan atapnya berbentuk segi-lima. Unsur yang dimiliki prisma segi-lima ABCDE.FGHIJ adalah sebagai berikut:
  • Sisi/bidang = memiliki 7 sisi atau bidang yaitu sisi alas (ABCDE), sisi atas (FGHIJ), Sisi tegak (ABGF, BCHG, CDIH, DEJI, AEJF)
  • Rusuk = memiliki 15 rusuk yaitu rusuk alas (AB, BC, CD, DE, EA), Rusuk atas (FG, GH, HI, IJ, JF) rusuk tegak (FA, GH, HI, IJ, JE)
  • Titik Sudut = memiliki 10 titik sudut yaitu titik sudut A, B, C, D, E, F, G, H, I, dan J

 4. Prisma Segi-n

Untuk prisma segienam, segitujuh,…., Segi-n anda dapat menggunakan
Banyak sisi/bidang prisma segi-n = n + 2
Banyak rusuk prisma segi-n = 3n
Banyak titik sudut prisma segi-n = 2n

Rumus Prisma

1. Volume Prisma

Untuk menghitung besar volume prisma digunakan rumus:

Volume = Luas alas x tinggi

Dimana tinggi adalah tinggi prisma
Misalnya:
Volume Prisma segitiga = Luas alas x t
                                                = (1/2xalasxtinggi) x t
Volume Prisma segiempat = Luas alas x t
                                                = (p x l) x t

 2. Luas permukaan prisma

Untuk menghitung luas permukaan prisma digunakan rumus:

Luas       = Jumlah luas bidang-bidang sisinya

   = Luas alas + luas atas + luas selubungnya


Tabung (geometri)



Sebuah tabung
Dalam geometri, tabung atau silinder adalah bangun ruang tiga dimensi yang dibentuk oleh dua buah lingkaran identik yang sejajar dan sebuah persegi panjang yang mengelilingi kedua lingkaran tersebut. Tabung memiliki 3 sisi dan 2 rusuk.
Kedua lingkaran disebut sebagai alas dan tutup tabung serta persegi panjang yang menyelimutinya disebut sebagai selimut tabung.

Rumus hitung silinder

Luas alas pada silinder

L = \pi r^2

Luas selimut

L = 2 \ \pi r \ h
....

Luas permukaan

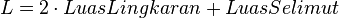
L = 2\cdot LuasLingkaran + LuasSelimut
    = 2\cdot \pi r^2 + 2 \pi r \cdot h, atau
    = 2\cdot \pi r\cdot (r + h)

Volume

V = \pi r^2 \cdot h
   = \frac{1}{4} \pi d^2 \cdot h

Kerucut



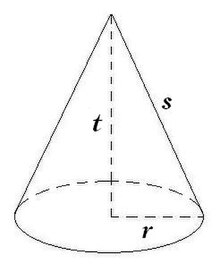
Sebuah kerucut dengan tinggi t dan garis pelukis s
Dalamgeometri, kerucut adalah sebuah limas istimewa yang beralas lingkaran. Kerucut memiliki 2 sisi dan 1 rusuk.
Sisi tegak kerucut tidak berupa segitiga tapi berupa bidang lengkung yang disebut selimut kerucut.

Rumus kerucut

Luas alas

L = \pi r^2

Luas selimut

L = \pi\ r\ s

Luas permukaan

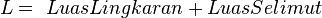
L = \ LuasLingkaran + LuasSelimut
    = \pi r^2 + \pi\cdot r\cdot s, atau
    = \pi r\cdot (r + s)

Volume

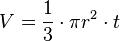
V = \frac{1}{3}\cdot \pi r^2 \cdot t



Diposting oleh di

1 komentar:

  1. haddasamacguire3 Maret 2022 pukul 09.33

    Betway Casino CT Bonus Code - JTAH Hub
    Betway 성남 출장마사지 Casino CT 속초 출장마사지 Bonus Code. Betway Casino CT 삼척 출장마사지 Bonus Code. Betway Casino CT bonus code. Betway Casino CT bonus code. Betway Casino CT bonus 세종특별자치 출장안마 code. Betway 나주 출장안마 Casino

    BalasHapus

Langganan: Posting Komentar (Atom)